摘要：透镜的棱镜效果公式描述了光线通过透镜产生的偏折角度，其公式基于透镜的折射率、透镜的形状和大小以及光线的入射角度等因素。该公式在光学领域具有广泛的应用，包括望远镜、显微镜、摄影镜头等光学仪器的设计和制造中。通过应用透镜的棱镜效果公式，可以实现光线的精确控制和调整，从而达到更好的成像效果和视觉体验。该公式还在激光技术、光学测量等领域发挥着重要作用。

本文目录导读：

1. 透镜棱镜效果的基本原理
2. 透镜棱镜效果公式
3. 透镜棱镜效果的应用

透镜作为光学器件的重要组成部分，其棱镜效果在光学领域中具有重要地位，透镜的棱镜效果是指光线通过透镜后发生偏转的现象，这一现象在日常生活和科研中有着广泛的应用，本文将详细介绍透镜棱镜效果的基本原理、公式及其应用。

透镜棱镜效果的基本原理

透镜棱镜效果的基本原理是光的折射，当光线从一种介质传入另一种介质时，由于两种介质的折射率不同，光线会发生传播方向的改变，这种现象称为光的折射，透镜通过改变光线的传播路径，实现对光线的聚焦和分散作用，从而产生棱镜效果。

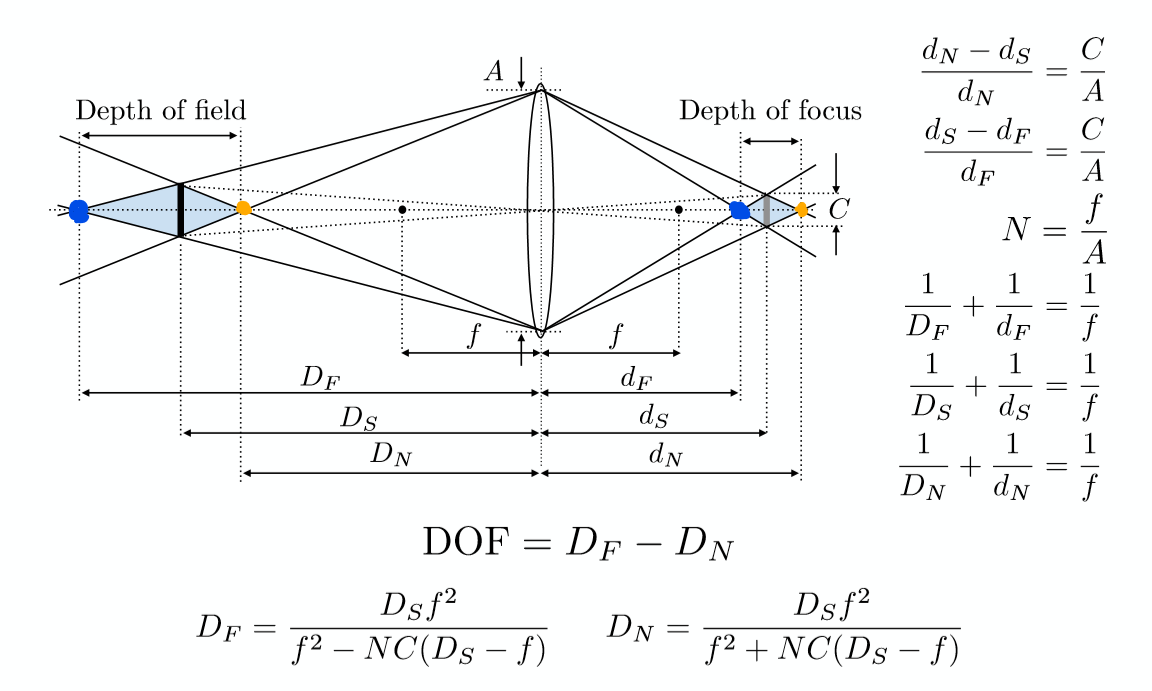
透镜棱镜效果公式

透镜棱镜效果可以通过公式进行计算，常用的公式有：

1、薄透镜公式：当光线通过薄透镜时，光线的偏转角度与透镜的折射率、厚度、入射角度等因素有关，薄透镜公式可用于计算光线通过薄透镜后的偏转角度，具体公式为：θ₁ = θ₀ × n × d / f，₁为出射光线与入射光线之间的夹角，θ₀为入射光线与透镜表面的夹角，n为透镜的折射率，d为透镜的厚度，f为透镜的焦距。

2、棱镜偏转公式：当光线通过棱镜时，光线的偏转角度与棱镜的形状、折射率等因素有关，棱镜偏转公式可用于计算光线通过棱镜后的偏转角度，具体公式为：θ = A + Δθ，为光线通过棱镜后的偏转角度，A为棱镜的顶角，Δθ为光线在棱镜中的折射角，不同类型的棱镜（如等腰棱镜、直角棱镜等）在应用中需要根据具体情况选择合适的公式进行计算。

透镜棱镜效果的应用

透镜棱镜效果在日常生活和科研中有着广泛的应用，以下是几个典型的应用实例：

1、眼镜：近视眼镜和老花眼镜利用透镜的棱镜效果，使光线在进入眼睛前发生偏转，从而使人能够清晰地看到远处的物体和近处的物体。

2、显微镜：显微镜中的物镜和目镜利用透镜的聚焦作用，结合棱镜效果，将微小的物体放大并呈现在观察者眼前。

3、摄影镜头：摄影镜头中的透镜通过棱镜效果调整光线的传播路径，从而实现拍摄清晰、高质量的图像。

4、光学仪器：许多光学仪器（如望远镜、测量仪器等）都利用透镜的棱镜效果来实现特定的功能，望远镜中的棱镜可以使光线发生偏转，增加观测视角；测量仪器中的棱镜可以用于精确测量距离和角度等参数。

5、激光技术：在激光技术中，透镜的棱镜效果用于调整激光束的传播方向，实现激光束的聚焦、分束和扫描等功能，棱镜还可以用于激光干涉仪等高精度测量设备中，提高测量精度和稳定性。

本文介绍了透镜棱镜效果的基本原理、公式及其应用，透镜的棱镜效果在日常生活和科研中具有重要的应用价值，涉及眼镜、显微镜、摄影镜头、光学仪器和激光技术等领域，了解透镜棱镜效果的基本原理和公式，有助于更好地理解和应用透镜，提高光学设备的性能和精度，未来随着科技的不断发展，透镜棱镜效果在更多领域的应用将不断得到拓展和创新。